Theoretical and modeling developments
Simulation tools
In order to interpret extinction and scattering single particle measurements (tightly focused light beam) several modeling approaches have been used:
- Analytical methods (home-written codes) based on the multipolar Mie theory and its various generalizations, which allow investigating systems consisting of interacting metal/dielectric spheres or layered structures as core-shell nanoparticles;
- Numerical methods which allow computing the optical response of nanoobjects of arbitrary shape (cross-sections, near-field and charge distributions).
Two numerical methods are used:
- Finite element method (FEM; COMSOL Multiphysics software) which consists in solving directly the Maxwell equations in the space domain;
- The Discrete Dipole Approximation (DDA) which consists in replacing each homogeneous medium by a large set of “polarizable points”.
In the frame of our works these various approaches are complementary, the analytical methods (of limited applicability) allowing to test the accuracy of the numerical methods in the case of systems involving strong coupling (for instance nanodimers near the conductive contact limit).
Effect of confinement on the broadening of the Localized Surface Plasmon Resonance (LSPR)
In the frame of collaboration with the FemtoNanoOptics team, the quantum finite size effects on the optical response of silver nanoparticles (diameter D < 15 nm) have been investigated exhaustively [Baida 2009]. This work aimed at studying the evolution, as a function of the particle diameter, of the LSPR bandwidth which is intimately related to the lifetime of the collective conduction electron excitation. The Time-Dependent Local Density Approximation (TDLDA) has been used for describing the optical response of the conduction electrons (collective excitations and particle-hole one-electron excitations) in the frame of a jellium-like model including the dielectric effects (polarization and absorption) arising from the core-electrons and the surrounding matrix. These investigations have allowed to bring to light the scaling law (linear with respect to 1/D) characterizing this broadening (Landau damping) and to quantify the confinement contribution to the experimental LSPR bandwidth (roughly 50 %, the additional contribution being –probably- related to the size dependence of the electron-phonon coupling) [Lermé 2010, Lermé 2011].
Substrate effects on the optical response of supported particles
The initial purpose of this theoretical investigation was to test the rather crude widespread hypothesis stating that the effect of a nearby dielectric substrate on the optical response of supported nanoparticles can be mimicked by an effective homogeneous surrounding medium. An exhaustive study has been carried out in the case of a spherical metal particle deposited on a dielectric interface, system for which the Maxwell equations can be solved exactly. The influence of numerous parameters have been investigated: material, substrate index, sphere radius, sphere-interface distance, irradiation conditions… In many cases the optical response exhibits a rich multipolar structure, differing strongly from that of a sphere embedded in a homogeneous medium (fig. 1). This complex structure, which results from the interaction of the metal sphere with its “image”, as well as the evolution as a function of the sphere-interface distance, can be analyzed in the frame of a hybridization model, similar to that developed for describing plasmonic couplings in the case of nanodimers [Lermé 2013].
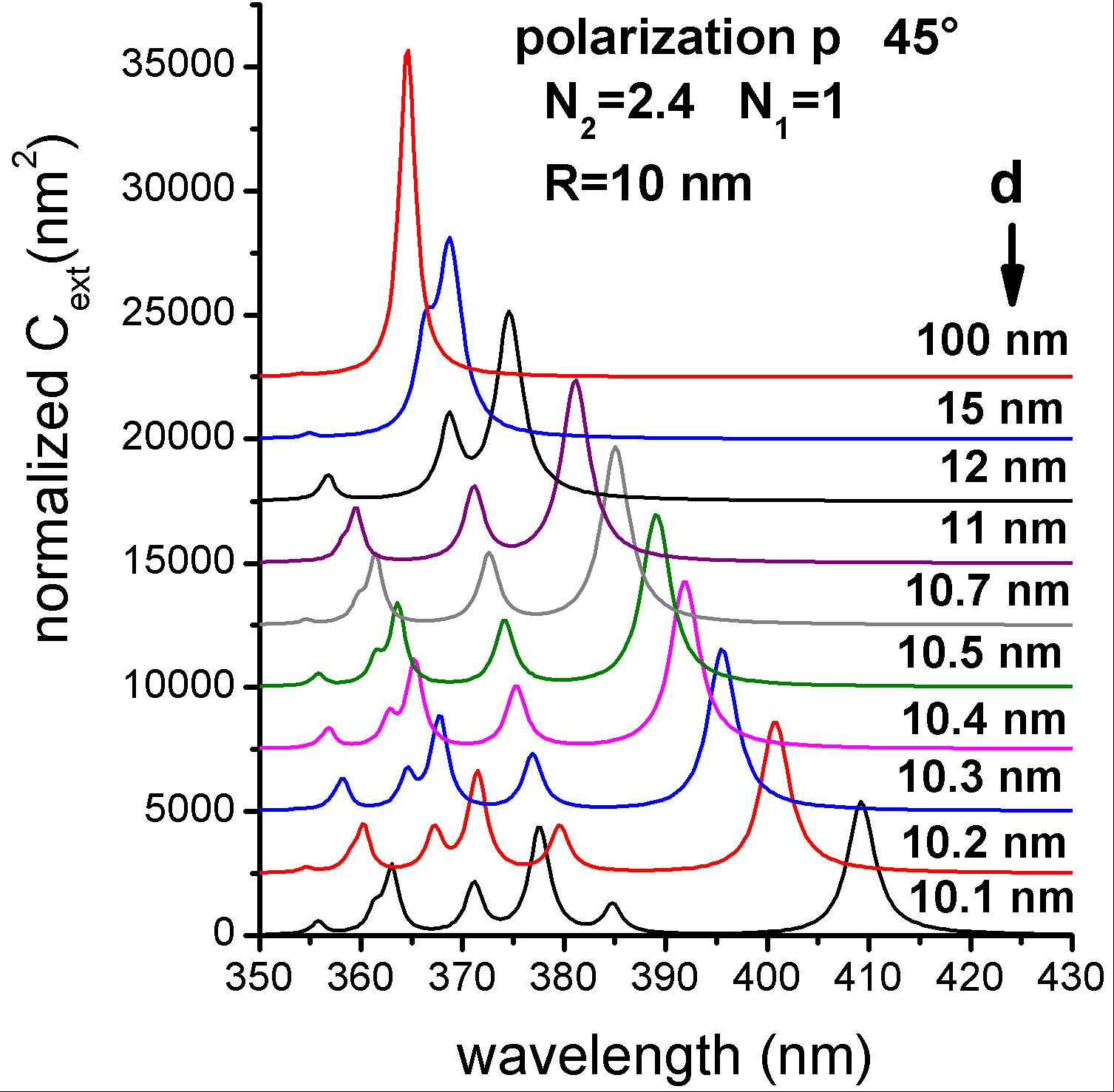
Fig. 1 : Extinction cross-sections of a silver sphere (D = 20 nm) in air (N1 = 1),
located above a substrate of optical index N2 = 2.4, as a function of the sphere-interface distance d.

















